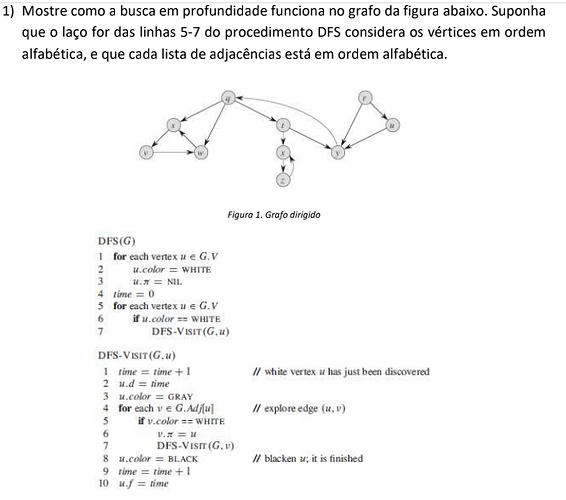
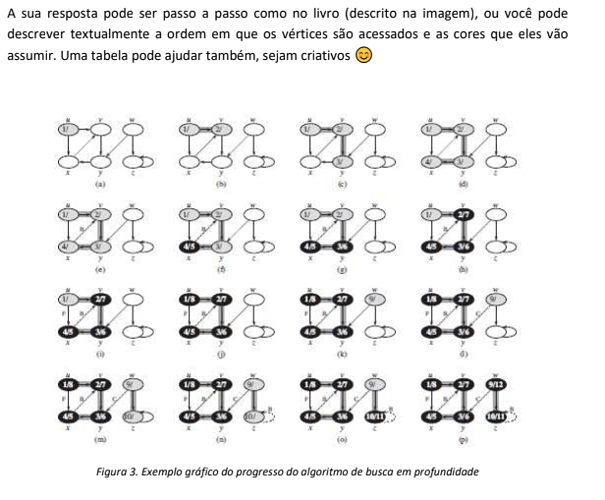
Pelo algoritmo, parece que esse é o livro do Cormen.
Note que cada vértice possui alguns atributos:
- color, que vai indicar se o vértice ainda não foi visitado (WHITE), se já foi visitado (BLACK) ou se ainda está sendo processado (GRAY);
- pi, que indica qual o vértice usado para chegar no vértice atual na árvore gerada pela busca em profundidade, ou seja, seu antecessor/pai;
- d, que indica a distância ou quantidade de pulos para sair do vértice fonte e chegar no vértice atual;
- time, indica a ordem de visita dos vértices.
G é o objeto do grafo e V é o atributo que contém a codificação das listas de adjacências mostradas abaixo, de acordo com o que é explicado no enunciado:
vértice -> lista de adjancências
q -> [s, t, w]
r -> [u, y]
s -> [v]
t -> [x, y]
u -> [y]
v -> [w]
w -> [s]
x -> [z]
y -> [q]
z -> [x]
Quando DFS(F) é invocado, um for é executado, percorendo todos os vértices do grafo (primeira coluna do esquema acima), marcando cada vértice como WHITE (não visitado) e seu antecessor como NIL (null, nulo). O tempo é zerado e agora, outro for é executado, percorrendo novamente todos os vértices, entrando no if somente se o vértice for branco. Caso o vértice seja branco, a parte recursiva do algoritmo é iniciada. A ideia da busca em profundidade é visitar sistematicamente todos os vértices do grafo e, para cada vértice visitado, verificar se há algum caminho a seguir a partir dele, ou seja, se há uma aresta do vértice atual para um outro vértice. Caso exista o caminho e o vértice de destino não esteja marcado como BLACK, o processo continua.
Para o exemplo o processo de busca se inicia no vértice q. q possui três vértices adjacentes: s, t e w. Como esse é um grafo dirigido/direcionado (digrafo) a aresta só tem uma direção.
Vou implementar em Java para vc entender.
Dê uma olhada:
/**
*
* @author Prof. Dr. David Buzatto
*/
public class GrafoExemplo {
private static enum Color {
WHITE,
GRAY,
BLACK
}
private static class Vertex {
String label;
Color color;
Vertex pi;
int d;
int f;
Vertex[] adj;
int i; // posição na lista de adjacências
Vertex( String label ) {
this.label = label;
}
@Override
public String toString() {
return label + " {color=" + color + ", pi=" + ( pi == null ? "null" : pi.label ) + ", d=" + d + ", f=" + f + '}';
}
}
private static class Digraph {
Vertex[] V;
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
if ( V != null ) {
System.out.println( "Digraph: " );
System.out.println( " v | pi | color | d | f" );
System.out.println( "----------------------------" );
for ( Vertex v : V ) {
System.out.printf( " %s | %s | %s | %02d | %02d \n",
v.label,
v.pi == null ? "null" : v.pi.label + " ",
v.color,
v.d,
v.f );
}
}
return sb.toString();
}
}
/**
* @param args the command line arguments
*/
public static void main( String[] args ) {
Vertex q = new Vertex( "q" );
Vertex r = new Vertex( "r" );
Vertex s = new Vertex( "s" );
Vertex t = new Vertex( "t" );
Vertex u = new Vertex( "u" );
Vertex v = new Vertex( "v" );
Vertex w = new Vertex( "w" );
Vertex x = new Vertex( "x" );
Vertex y = new Vertex( "y" );
Vertex z = new Vertex( "z" );
q.adj = new Vertex[]{ s, t, w };
r.adj = new Vertex[]{ u, y };
s.adj = new Vertex[]{ v };
t.adj = new Vertex[]{ x, y };
u.adj = new Vertex[]{ y };
v.adj = new Vertex[]{ w };
w.adj = new Vertex[]{ s };
x.adj = new Vertex[]{ z };
y.adj = new Vertex[]{ q };
z.adj = new Vertex[]{ x };
Digraph G = new Digraph();
G.V = new Vertex[]{ q, r, s, t, u, v, w, x, y, z };
DFS( G );
System.out.println( G );
}
private static int time;
public static void DFS( Digraph G ) {
for ( int i = 0; i < G.V.length; i++ ) {
Vertex u = G.V[i];
u.color = Color.WHITE;
u.pi = null;
u.i = i;
}
time = 0;
for ( Vertex u : G.V ) {
if ( u.color == Color.WHITE ) {
DFSVisit( G, u, "" );
}
}
}
private static void DFSVisit( Digraph G, Vertex u, String recuo ) {
System.out.println( recuo + "Visitando " + u );
u.d = ++time;
u.color = Color.GRAY;
System.out.println( recuo + "Processando " + u );
System.out.println( recuo + "Adjacentes de " + u.label );
for ( Vertex v : G.V[u.i].adj ) {
if ( v.color == Color.WHITE ) {
v.pi = u;
DFSVisit( G, v, recuo + " " );
}
}
u.color = Color.BLACK;
u.f = ++time;
System.out.println( recuo + "Processado " + u );
}
}
Ao executar, o resultado é o seguinte:
Visitando q {color=WHITE, pi=null, d=0, f=0}
Processando q {color=GRAY, pi=null, d=1, f=0}
Adjacentes de q
Visitando s {color=WHITE, pi=q, d=0, f=0}
Processando s {color=GRAY, pi=q, d=2, f=0}
Adjacentes de s
Visitando v {color=WHITE, pi=s, d=0, f=0}
Processando v {color=GRAY, pi=s, d=3, f=0}
Adjacentes de v
Visitando w {color=WHITE, pi=v, d=0, f=0}
Processando w {color=GRAY, pi=v, d=4, f=0}
Adjacentes de w
Processado w {color=BLACK, pi=v, d=4, f=5}
Processado v {color=BLACK, pi=s, d=3, f=6}
Processado s {color=BLACK, pi=q, d=2, f=7}
Visitando t {color=WHITE, pi=q, d=0, f=0}
Processando t {color=GRAY, pi=q, d=8, f=0}
Adjacentes de t
Visitando x {color=WHITE, pi=t, d=0, f=0}
Processando x {color=GRAY, pi=t, d=9, f=0}
Adjacentes de x
Visitando z {color=WHITE, pi=x, d=0, f=0}
Processando z {color=GRAY, pi=x, d=10, f=0}
Adjacentes de z
Processado z {color=BLACK, pi=x, d=10, f=11}
Processado x {color=BLACK, pi=t, d=9, f=12}
Visitando y {color=WHITE, pi=t, d=0, f=0}
Processando y {color=GRAY, pi=t, d=13, f=0}
Adjacentes de y
Processado y {color=BLACK, pi=t, d=13, f=14}
Processado t {color=BLACK, pi=q, d=8, f=15}
Processado q {color=BLACK, pi=null, d=1, f=16}
Visitando r {color=WHITE, pi=null, d=0, f=0}
Processando r {color=GRAY, pi=null, d=17, f=0}
Adjacentes de r
Visitando u {color=WHITE, pi=r, d=0, f=0}
Processando u {color=GRAY, pi=r, d=18, f=0}
Adjacentes de u
Processado u {color=BLACK, pi=r, d=18, f=19}
Processado r {color=BLACK, pi=null, d=17, f=20}
Digraph:
v | pi | color | d | f
----------------------------
q | null | BLACK | 01 | 16
r | null | BLACK | 17 | 20
s | q | BLACK | 02 | 07
t | q | BLACK | 08 | 15
u | r | BLACK | 18 | 19
v | s | BLACK | 03 | 06
w | v | BLACK | 04 | 05
x | t | BLACK | 09 | 12
y | t | BLACK | 13 | 14
z | x | BLACK | 10 | 11
Foram encontrados dois componentes conexos (duas árvores):
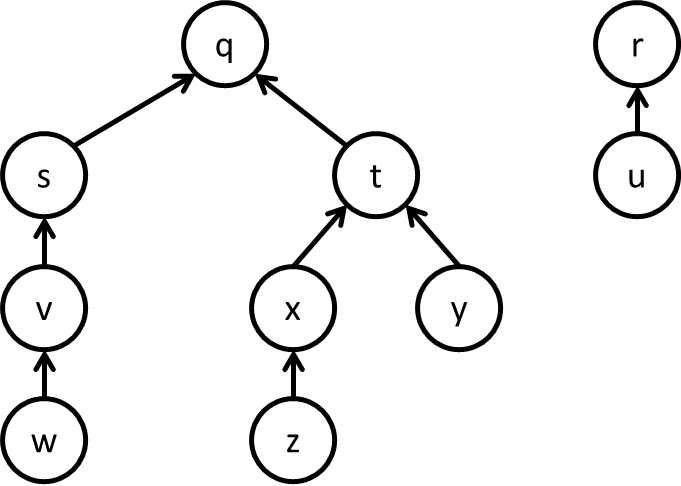
Eu não uso o livro do Cormen para dar aula de algoritmos e estruturas de dados, mas se vc assistir minha aula talvez fique mais fácil. Meu livro favorito e que eu adoto é o Algorithms do Robert Sedgewick. Nesse livro, a implementação dos algoritmos em grafos codifica os atributos dos vértices em arrays auxiliares.
Aqui você pode pegar a explicação só do algoritmo de busca em profundidade. Se assistir a aula inteira eu trato de grafos do início até a busca de componentes conexos.