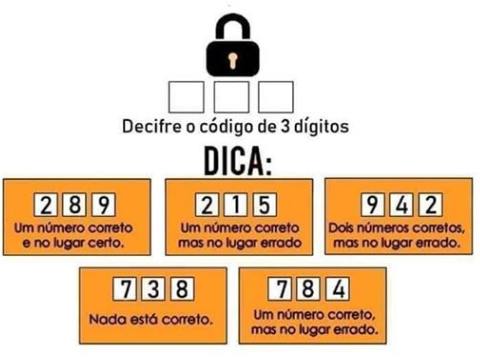
Pessoal, tem essa brincadeira de descobrir os 3 dígitos do cadeado com as pistas.
Teve um programador que desenvolveu um código para isso. Para quem tá começando como eu, esse código é bem complexo. Fico imaginando desenvolver isso. Alguém se arrisca a explicar?
import java.util.stream.IntStream;
public class Test {
public static void main(String[] args) {
for (int i = 1; i <= 999; i++) {
String s = String.format("%03d", i);
int[] arr = {s.charAt(0) - '0', s.charAt(1) - '0', s.charAt(2) - '0'};
if (test01(arr) && test02(arr) && test03(arr) && test04(arr) && test05(arr)) {
System.out.println("resultado: " + s);
}
}
private static boolean test01(int[] arr) {
return (arr[0] == 2 && arr[1] != 8 && arr[2] != 9)
|| (arr[1] == 8 && arr[0] != 2 && arr[2] != 9)
|| (arr[2] == 9 && arr[0] != 2 && arr[1] != 8);
}
private static boolean test02(int[] arr) {
return umNumeroCorretoNoLugarErrado(arr, new int[]{2, 1, 5});
}
private static boolean test03(int[] arr) {
int[] idxOf = {
indexOf(9, arr),
indexOf(4, arr),
indexOf(2, arr)
};
int[][] grid = {{0, 1, 2}, {1, 0, 2}, {2, 0, 1}};
int[] arr2 = {9, 4, 2};
for (int[] idx : grid) {
if (idxOf[idx[0]] >= 0 && idxOf[idx[1]] >= 0 && idxOf[idx[2]] < 0) {
return arr[idx[0]] != arr2[idx[0]] && arr[idx[1]] != arr2[idx[1]];
}
}
return false;
}
private static boolean test04(int[] arr) {
return indexOf(7, arr) < 0
&& indexOf(3, arr) < 0
&& indexOf(8, arr) < 0;
}
private static boolean test05(int[] arr) {
return umNumeroCorretoNoLugarErrado(arr, new int[]{7, 8, 4});
}
private static boolean umNumeroCorretoNoLugarErrado(int[] arr, int[] arr2) {
int[] idxOf = {
indexOf(arr2[0], arr),
indexOf(arr2[1], arr),
indexOf(arr2[2], arr)
};
if (IntStream.of(idxOf).allMatch(n -> n < 0)) {
return false;
}
int[][] grid = {{0, 1, 2}, {1, 0, 2}, {2, 0, 1}};
for (int[] idx : grid) {
if (idxOf[idx[0]] >= 0) {
if (idxOf[idx[1]] >= 0 || idxOf[idx[2]] >= 0) {
return false;
}
return arr[idx[0]] != arr2[idx[0]];
}
}
return false;
}
private static int indexOf(int n, int[] arr) {
for (int i = 0; i < arr.length; i++) {
if (arr[i] == n) {
return i;
}
}
return -1;
}
}
@author Vinicius Silva