Dúvida sobre curvas B-Splines

Programação
#1

Basicamente, eu estou implementando um código para gerar curvas B-Splines de ordem k no Octave dados vetores X e Y com as coordenadas dos pontos críticos, um vetor U com os nós e N passos

function [SX SY] = Spline_Curve(X, Y, U, N)
  
  n = length(X)-1;
  
  for i = 0:N
    t = i/N;
    [SX(i+1) SY(i+1)] = Spline(n,X,Y,U,t);
  endfor
  return
end

A função Spline faz o somatório dos termos

function [PX PY] = Spline(n,X,Y,U,t)
  PX = 0;
  PY = 0;
   
  m = length(U)-1;
  k = m-n-1;
   
  for i = 0:k
       
    S = Spline_Nucleo(U,i+1,t,k);
    PX = PX + X(i+1)*S;
    PY = PY + Y(i+1)*S;
  endfor
end

Por fim, a Spline_Nucleo calcula os termos que vão para o somatório de maneira recursiva

function [S] = Spline_Nucleo(U,i,t,k)
    
  if (k == 0)
    if U(i) <= t < U(i+1)
      S = 1;
    else
      S = 0;
    endif
  else
    esq = 0;
    if (U(i+k) - U(i) != 0)
      esq = (t - U(i))/(U(i+k) - U(i))*Spline_Nucleo(U,i,t,k-1);
    endif

    dir = 0;
    if (U(i+k+1) - U(i+1) != 0)
      dir = (U(i+k+1) - t)/(U(i+k+1) - U(i+1))*Spline_Nucleo(U,i+1,t,k-1);
    endif

    S = esq + dir;
  endif
    
end

O problema é que no teste que eu fiz com U = {0, 0, 0, 1, 2, 3, 4, 5, 6, 6, 6}, X = {1, 2, 4, 7, 7.5, 5, 4.5, 6} e Y = {0, 1, 0, 1, 3, 3.5, 2, 2.5} com N = 50 obtive

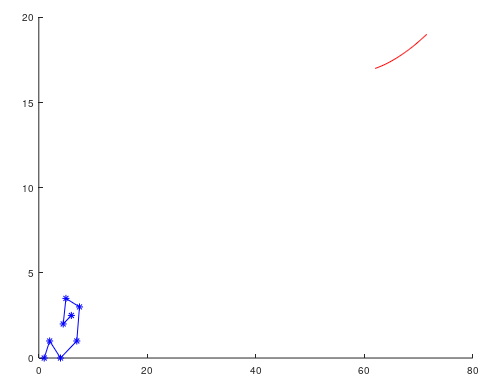
Captura%20de%20tela%202021-06-24%20230002

Alguém sabe se é algum problema com o código? Estou me confundindo nos índices do núcleo? Ou é problema com a teoria mesmo?

#2

Cara, desculpe a minha ignorância, mas nunca mexi com isso que vc está tentando fazer, mas achei uma implementação em python com uma imagem mostrando o resultado. Talvez vc possa dá uma conferida: https://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.BSpline.html

Ah sim. Como vc está testando isso e qual linguagem é essa?

#3

Muito obrigado! Não tinha encontrado essa implementação quando estava pesquisando.

Eu estou testando fornecendo vetores de pontos para o programa com algumas formas que eu já sei o que deveriam dar e essa linguagem é Octave.