Sei que não é o escopo do fórum, mas alguém consegue me ajudar nesse cálculo de limite?
Fórmula:
lim 2.209 - sqrt( x + 2209 ) / x
x -> 0
Segue anexo a imagem da fórmula (imagem 1), e a parte do cálculo que eu “tranquei” (imagem 2).
P.S1: A formula ta escrita em forma de “programaçao”, ja que nao tenho como representar a sintaxe correta aqui.
P.S2: Caso não seja adequado removo esse tópico.
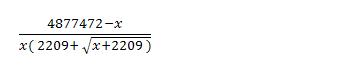
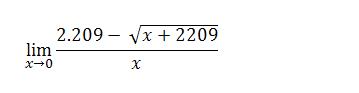
Fala RafaelViana
Nesse caso, fazendo diretamente, teremos (2.209 - sqrt(2209 + 0))/0. Com temos uma quantidade finita sendo dividida por 0, esse limite vai tender ao infinito quando x tender a 0.
Opa… valeu.
Então, o professor deve ter se enganado nesse enunciado, pois ainda não nos explicou essa situação.
Eae matheuslmota
Tipo, sou colega do Rafael, tbem tô com o mesmo problema. E tava pensando em responder como
se o limite quando tende a 0, não existisse.
Isso pode ser a resposta d uma questão??
obrigado.
Cara vejamos. O limite é uma situação que acontece quando temos uma função e aproximando “x” para um determinado valor, a função passa a se aproximar de um determinado valor sem no entanto, atingi-lo.
Por exemplo:
y = x * 2;
Se nós aproximarmos x de 5, y vai tender a 10, sem no entanto atingi-lo.
No caso do problema de vocês, vou supor a seguinte função:
y = 2 / x;
para x -> 0;
Perceba que x vai se aproximar de 0 e nao vai atingir 0.
Se x = 0.1, y = 20;
Se x = 0.01, y = 20;
Se x = 0.0000000000001, y = 20000000000000;
Perceba que quanto mais x se aproxima de 0, mas a função vai tendo para um numero grande.
No limite, com x-> 0, y -> infinito.
Essa é a solução.
Vocês estão no começo da cadeira de cálculo sim?
A única solução para esse problema é essa.
sim estamos…
valeu pela ajuda.
disponha.
Entendido 
Tambem, achei um exemplo que ilustra isso no site da USP:
http://ecalculo.if.usp.br/ferramentas/limites/calculo_lim/exemplos/exemplo4.htm
